Kayıp Gezegen Vulcan
1859 senesi ile 2006 senesinin ortak yanı nedir? Bir çok cevabı olabilir. Ancak bu soruyu cevaplamanın belki de en ilginç yolu her ikisinde de güneş sistemimizde gezegen olduğu kabul edilen gök cismi sayısının dokuz olduğu bir dönem bulunduğunu söylemektir.
1859 yılında varlığını bildiğimiz gezegenlere şöyle bir bakalım: Güneş'e en yakından başlarsak altı gezegen, yani Merkür, Venüs, Dünya, Mars, Jüpiter ve Satürn zaten antik zamandan beri biliniyordu (Dünya'nın yaklaşık iki bin sene kadar gezegen kabul edilmediğini biliyoruz, ancak bu başka bir yazının konusu). Teleskoptan sonraki dönemde ise iki gezegen, 1781'de Uranüs ve 1846'da Neptün, bulunmuştu. Dolayısıyla sekiz gezegen cepteydi. 2006'nın ikinci yarısında Uluslararası Astronomi Birliğinin kararıyla gezegenlik statüsünden çıkarılan Pluton'u da eklersek dokuzu tamamlıyoruz, peki bunun neresi ilginç? Şurası: Pluton 1859'da henüz keşfedilmemişti ve bir yetmiş yıl daha keşfedilemeyecekti. Öyleyse, dokuzuncu gezegen eğer Pluton değilse hangisiydi ve şu an nerede?
Bu yazıda bilim tarihindeki en enteresan anekdotlardan biri olan kayıp gezegen Vulcan'ın hikayesini anlatacağım. Sahi bir şey hiç var olmamışsa kaybolabilir mi, yoksa önce bulunması mı gerekir? Peki olmayan bir şey nasıl bulunur? Unutmayın evin anahtarından değil, güneş sistemimizdeki koca bir gezegenden bahsediyoruz, bunlar sormaya pek de alışık olduğumuz sorular değil.
Vulcan, Güneş sistemimizde Merkür ve Güneş arasında yer alan, zamanında herkesin varlığına inandığı, astronomların gözlediği, gazetelerin ise haberlerini yaptığı, ancak aslında hiç var olmamış bir gezegendi. İsmini Güneş'e olan yakınlığından dolayı Roma mitolojisindeki Ateş Tanrısından almıştı. Bu sıcak gezegen 26 Mart 1859'da Fransız amatör astronom Edmond Modeste Lescarbault tarafından keşfedilmişti.
Lescarbault'un gözlemlerinde aldığı notlardan, daha sonra zamanın ünlü Fransız astronomu Le Verrier tarafından hesaplandığı üzere, Vulcan Güneş'ten 0.147 AU mesafedeydi ve Güneş etrafındaki bir turu 19 gün 17 saat sürüyordu. Yörüngesi ekliptiğe göre 12 derece 10 dakika kadar eğikti. Daha önce görülmediğine göre Merkür'den daha karanlık bir gezegen olmalıydı. Vulcan her sene 3 Nisan ile 6 Ekim arasında Güneş'in önünden en az iki, genellikle ise dört kez geçmeliydi. Tüm bu teknik detaylara ve hesaplamalara bakılırsa Vulcan hakkında bilmediğimiz bir şey yok gibiydi. Üstelik, Le Verrier'in, Lescarbault'un gözlemlerine dayanarak yaptığı bu açıklamalar sonrasında bir çok tanınmış ve güvenilir astronom kendi gözlem notlarına bakarak bu gezegeni aslında Lescarbault'tan daha önce görmüş ve defterlerine kaydetmiş olduklarını fark ettiler ve bunu açıkça beyan ettiler. Tek problemse Vulcan diye bir gezegenin hiç bir zaman var olmamış olmasıydı. Peki tüm bunların açıklaması neydi? Bu açıklamayı yapmamız için biraz eskiye, Kepler ve Newton zamanlarına gitmemiz ve tarihte yavaş yavaş ilerlememiz gerekiyor.
Kepler ve Newton
Kepler'in (1571-1630) gezegenlerin hareketine dair üç yasası şöyle özetlenebilir: (1) tüm gezegenlerin yörüngeleri, bir odağında Güneş olan elipslerdir, (2) Güneş'ten gezegene uzanan bir çizgi, eşit zamanlarda eşit alanlar süpürür ve (3) tüm gezegenlerin yörüngelerindeki bir turu için geçen sürenin karesi ile elipsin merkezine olan mesafenin küpü aynıdır.
Kepler'in bu üç yasasının bilmemiz gereken önemli bir özelliği var: bu üç yasa tamamen ve yalnızca gözlemlere dayanıyor. Peki bu tam olarak ne anlama geliyor? Kısacası, Kepler gökyüzüne bakmış, incelemiş, notlar almış, gezegenlerin ne zaman nerede göründüklerini kaydetmiş ve en sonunda bunları bir eğri üzerine oturttuğunda yörüngelerinin bir elipsi oluşturduğunu görmüştü. Tabi Kepler'in bunları yaparken zamanının en iyi gözlemlerini yapan meşhur astronomu Danimarkalı Tycho Brahe (astronomi merkezi Uraniborg'un kurucusu ve yöneticisi) ile çalıştığını ve bu sayede eline son derece keskin, kesin ve hassas ölçümler sonucu oluşturulmuş verilerin geçtiğini bilmemiz gerekir. Aynı şekilde, Kepler'in 2. ve 3. yasaları da bu şekilde gökyüzü gözlemlerinden yapılan genellemelerden ibaretti ve elindeki verileri nasıl formüle edebileceğini araştırarak bu sonuçlara ulaşabilmişti. Örneğin (2) no'lu yasanın geçerli olması için gezegenlerin Güneş'e yakınken hızlı ve Güneş'ten uzakken daha yavaş hareket ettiğini fark etmesi doğal olarak gerçekleşiyordu zaten. Aynı şekilde gezegenlerin periyotlarını ve Güneş'e olan mesafelerini irdelediğinde tüm gezegenlerde bunların belli derecelerden oranlarının aynı olduğunu fark etmişti (3. yasa). Burada dikkat etmemiz gereken husus şu: Kepler gezegenlerin yörüngesinin elips olduğunu söylemişti, ama onun neden elips olduğu üzerine ya da nasıl bir sistemde eliptik bir yörünge oluşacağı üzerine bir şey söyleyememişti. Bunun için Newton'u beklememiz gerekecekti.
Newton 1687'de, başyapıtı Principia Mathematica'da, hareketin 3 kanununu lisede hepimizin öğrendiği üzere şu şekilde belirtmişti: (1) Her obje, üzerine bunu değiştirecek bir kuvvet uygulanmadıkça ya durağan halde bulunur ya da düz bir çizgi üzerinde düzgün hareket eder-eylemsizlik yasası, (2) Kuvvet, zaman içerisinde momentumdaki değişime eşittir ve (3) Her etkiye karşı eşit ve zıt bir tepki vardır. Newton ayrıca, bunlara ek olarak, Kepler'in 2. ve 3. yasalarını kullanarak kütle çekim kanununu da-yani temelde bir yıldız ve bir gezegen arasındaki kütle çekimi kuvvetinin büyüklüğünün kütlelerinin çarpımıyla doğru, aralarındaki mesafenin karesiyle ters orantılı olması (burada bahsedilen kuvvet gezegen ve yıldızın merkezlerini birleştiren doğru üzerinde etkir)-bulmuştu. Newton daha sonra hareketin 3 kanunu ve kütle çekimi kanununu kullanarak bunların gezegenlerde eliptik yörüngelere neden olacağını da göstermişti, ama bu başka bir yazının konusu.
Newton'un harekete dair kanunları ile Kepler'inkiler doğaları açısından birbirlerinden çok ayrıdır. Kepler yalnızca noktaları birleştirmiş, gözlemsel sonuçlara varmıştı ve söyledikleri yalnızca gezegenlerin hareketi için geçerliydi çünkü gözlemleri orayla sınırlıydı. Newton'un kanunları ise doğanın fiziksel yapısı hakkında hipotezlerdi ve basit gözlemlerden (Kepler'in yaptığı da tabi ki çok değerli) çok fazlasıydı. Üstelik bunlar yalnızca gezegenlerin hareketleriyle sınırlı olmayıp onlar da dahil olmak üzere her türlü hareket için geçerli olma iddiasındaki evrensel kurallardı. Newton'un kanunlarının (ya da hipotezlerinin) sınanmaya ihtiyacı vardı. Geçerlilikleri, test edilmelerine, çürütülmeye çalışılmalarına ve en sonunda tüm bu testleri başarıyla atlatabilmelerine bağlıydı. Yani Popper'ın 'falsification' dediği bilimin yanlışlanabilir olma özelliğine (ve aslında Popper'dan daha önce Einstein'ın 'Induction and Deduction in Physics' isimli makalesinde yazdığı gibi "bir teorinin doğruluğu asla kanıtlanamaz" ancak yanlışlığı gösterilebilir, ilkesine.)...
Newton Mekaniği ve Önemli Sınamalar
Newton'un harekete dair bu meşhur kanunları tarihte önemli sınamalardan geçti. Bu yazıda bunlardan beş tanesine bakacağız: (1) Ay Problemi (2) Halley Kuyrukluyıldızı'nın Yörüngesi (3) Jüpiter ve Satürn Eşitsizliği (4) Uranüs'ün Genişleyen Yörüngesi (5) Merkür'ün Yörünge Kayması
(1) Ay Problemi
Ay Problemi 1749'da, ancak Newton öldükten yirmi yıl kadar sonra çözülebildi. Problem şuydu: Bugüne kadarki gözlemlere göre, Ay'ın Dünya çevresinde takip ettiği yörüngeye baktığımızda Dünya'ya en yakın ve en uzak olduğu noktaları birleştiren doğru (yani yukarıdaki resimdeki 'Line of Apsides') her ay Ay'ın döndüğü yönde 3° 23' ilerlemekteydi. Newton ise 'matematiğe' yani kendi teorisine göre hesapladığında bunun 1° 31' 14'' olması gerektiğini görmüştü (Kepler'den farkı burada, Newton bir sistem kurup buna göre ne olması gerektiğini hesaplıyor, Kepler ise gözlem yapıp sonucunda gözlemlerinin uyduğu formülü açıklıyor). Yani teori ve gözlem uyuşmuyor.
Euler 1747'de "Ay'a etkiyen kuvvetlerin Netwon'un kurallarına uymadığını gösteren bir çok kanıt sunabilirim" dediğinde işte bu durumu kastediyordu. Aynı şekilde Clairaut, Newton'un kurallarının yanlış olduğuna atıf yaparak ters kare kuralının terk edilmesi gerektiğini belirtiyordu. Peki Newton gerçekten hatalı mıydı? Newton mekaniği yanlış mıydı? Gözlemler ve teori neden birbirini tutmuyordu?
Newton bu problemi çözmeye çalışırken, bize lisede ve örgün öğretimin çeşitli aşamalarında da öğretildiği gibi bazı varsayımlar yapıyordu. Örneğin, nasıl ki biz problemlerde pi'yi bazen iki basamağına kadar alırız, yuvarlarız ya da bazen çok küçük bazı değerlerin etkisini sonuca anlamlı etkisi olmayacağı ve hesabı çok zorlaştıracağı için 'ihmal edilebilir' diyerek göz ardı ederiz, aynı şekilde Newton da Ay'ın yörüngesini kendi kanunları kapsamında hesaplarken bazı varsayımlarda bulunmuştu. Hesaplarında, Ay'ın Dünya'ya göre relatif hareketi Güneş ile kıyaslandığında çok daha hızlı olduğu için Güneş'in pozisyonunu 'uzakta sabit bir nokta' olarak almıştı. Ancak sonrasında (görmeye kendi ömrü vefa etmese de) aslında Güneş'in hareketinin ihmal edilebilir olmadığı ortaya çıkmıştı.
Bu problemi 1749'da çözen Clairaut, Güneş'in pozisyonunu sabit olarak almadan Newton mekaniğine dayalı kapsamlı bir analize girişmişti. Newton kurallarından sapmadan, bu şekilde yaptığı hesaplamaları sonucunda görmüştü ki Ay Dünya'dan en uzak noktadayken Güneş'in hareketi ile aynı yönde olduğu için 'line of apsides' ilerlemekte, Ay Dünya'ya en yakındayken ise Güneş'in hareketi ters yönde olduğu için gerilemekteydi. Oluşan bu eşitsizlik sonucunda daha çok eşitsizlik oluşuyor ve bu ikincil dereceli etkiler toplandığında gözlem sonucu ile hesaplama sonucu birbirini sonunda tutuyordu. Yani hatalı olan Newton mekaniği değil, hesaplamalar yapılırken 'ihmal edilebilir' diye sınıflandırılan, ama aslında 'ihmal edilemeyecek olan' bir takım varsayımlardı.
Ay problem çözülmüştü. Astronom Robert Grant'ın özetlediği gibi "Newton'un teorisini tamamen çökertebilecek bu problem sonunda onun doğruluğunun en büyük göstergelerinden biri olarak sonuçlanmıştı".
(2) Halley Kuyrukluyıldızı'nın Yörüngesi
Sivri eliptik yörüngesi nedeniyle Güneş Çevresindeki hareketinde Neptün'den bile uzaklara ulaşan (resimdeki kırmızı rota) Halley Kuyrukluyıldızı Dünya'dan yaklaşık her 75 yılda bir çıplak gözle görülebiliyor. İlk kayıtları Çin'de M.Ö. 239 civarında tutulan Halley o zamandan bu yana defalarca kez bizi ziyaret etti, etmeye de devam ediyor. Astronomlar uzun süreler bu kuyrukluyıldızın yörüngesini hesaplamaya ve tam olarak ne zaman geri geleceğini tahmin etmeye çalıştılar.
Newton sonrası yakın geçmişe baktığımızda, Ay problemini çözen Clairaut da Halley'in ne zaman döneceğini hesaplamaya çalışanlardandı. Daha önce 1531, 1607, 1682'de geldiğini ve günberi (Güneşe en yakın olduğu konum) pozisyonuna ulaştığını biliyordu. Yani her geldiğinde tam aynı olmasa da yaklaşık 75 ya da 76 senelik bir periyotu var gibiydi. Ancak tam olarak hangi ayın hangi günü geleceğini ve günberiye ulaşacağını kestirmek henüz mümkün olmamıştı ve astronomlar arasında bu popüler ve çözene prestij kazandıracak bir problemdi.
Newton'un çağdaşı, Principia'nın yayımcısı ve kendisinin az sayıdaki arkadaşlarından biri olan Edmond Halley (bu kuyrukluyıldıza ismi verilen şahıs), Halley'in 1682'de günberiye ulaşmadan önce 1681'de Jüpiter'e fazlaca yaklaştığını fark etmişti. Kuyrukluyıldız, Jüpiter'in kütle çekiminden etkilenmiş ve yörüngesi bir miktar genişlemek zorunda kalmıştı. Dolayısıyla bir sonraki gelişinin gecikmesi beklenen bir şeydi. Ama ne kadar? Halley, 1758'in sonu ya da sonraki senenin başında geleceğini tahmin etmişti.
Ay probleminden tecrübeyle bazı hesaplamalarda ihmal edilebilir görülen şeylerin aslında nasıl ihmal edilemez olduğunun farkında olan Clairaut ise kuyrukluyıldızın yörüngesinde bir kaç gün arayla pozisyonlarının ve her pozisyonda Jüpiter ve Satürn gibi dev gezegenlerden mesafesinin hesaplanması gerektiğini ve bu şekilde bunların yörünge üzerindeki etkisinin görülebilieceğini düşünüyordu. Hesaplamanın doğru sonuç vermesi için Jüpiter ve Satürn'ün etkisinin tüm yörünge üzerine yedirilmesi gerekliydi. Hatta, Jüpiter'in Güneş'e uyguladığı çekim kuvveti bile 'ihmal edilmemeliydi'. Çünkü Güneş'in pozisyonundaki en ufak bir değişiklik bile kuyrukluyıldızın yörüngesinde anlamlı bir fark yaratabilirdi.
Clairaut, Newton mekaniğine dayanan kapsamlı hesaplamaları neticesinde Halley'in 1759 Nisan ayı ortası civarında (+/- 1 ay toleransla) günberiye ulaşacağını açıkladı. Bir aylık tolerans aslında 1682 yılındaki gözlem kayıtlarındaki olası hatalara dayanıyordu. Clairaut'un ve dayandığı Newton kanunlarının doğruluğu bir kez daha, Halley'in 13 Mart 1759'da günberiye ulaşmasıyla desteklenmiş oldu. Bir kez daha gözlemler ile teori birbiriyle uyuşmuştu. Evrensel kütle çekimi teorisi bir kez daha başarmıştı (kanıtlanmış oldu diyemiyoruz, çünkü bir teori ancak çürütülebilir, fakat kanıtlanamaz - ama desteklenebilir).
(3) Jüpiter ve Satürn Eşitsizliği
Jüpiter ve Satürn'ün yörüngelerinde Newton kanunlarına dayanan hesaplamalara bakıldığında yanlış bir şeyler vardı. Antik ve modern gözlemlere bakıldığında Jüpiter yavaş, Satürn ise olması gerekenden hızlı görünüyordu. Astronomları düşündüren bu problem Newton'dan sonra 1700'lerin sonuna kadar henüz çözülmüş durumda değildi. Aslında, bu problemin kaynağı gezegenlerin birbirleri üzerindeki çekim kuvvetlerinin uzun vadelerde yörüngelerinde yarattığı düzensizliklerdi. Tüm 17. yüzyıl boyunca Satürn'ün periyotu artmış ve Jüpiter'inki ise kısalmıştı. Satürn devamlı olarak hesaplanan yörüngesinden geride kalıyordu. Jüpiter ise kendi hesaplı yörüngesinden önde gidiyordu. Öte yandan tüm 18. yüzyıl boyunca ise bunun tam tersi olmaktaydı.
Problemi 1784'te yine Newton mekaniği ile çözen Laplace oldu. Açıklaması şöyleydi: Jüpiter'in Güneş çevresindeki hareketinin periyotunun 5 katı Satürn'ün periyotunun 2 katıyla denk durumdaydı (bunu Kepler'in 3. kanunu ile de basitçe hesaplayabiliriz). Bu demek oluyor ki Jüpiter (1 yılı Dünya'nın ~12 yılına eşit) ve Satürn (1 yılı Dünya'nın ~30 yılına eşit) her 5 Jüpiter yılı ve 2 Satürn yılı sonrasında yani bizim dilimizle 60 yılda bir döngülerinde aynı çizgi üzerinde buluşuyorlardı. Bu buluşmanın ve yakınlaşmanın kütle çekim anlamında kümülatif etkisi ise Laplace'ın Newton kanunları ile hesapladığı üzere, yörüngelerde gözlemlenen oldukça büyük bir düzensizlik oluyordu. Böylece, bir kez daha uzun zamandır bilinen bir problem, Newton mekaniği ile çözülmüş oluyordu.
(4) Uranüs'ün Genişleyen Yörüngesi
18. yüzyıl sonlarında, zamanının ünlü astronomu Herschel tüm gökyüzünü sistematik bir şekilde tarayarak her şeyi not etmeye ve gökyüzünün tam bir haritasını oluşturmaya karar vermişti. Bu çabalarının neticesinde 1781 yılında daha önce farkında olmadığımız bir gezegeni, yani bugünkü Uranüs'ü bulmuştu. Herschel'in bu keşfi neticesinde kendi gözlem kayıtlarına bakan bazı astronomlar Uranüs'ü kendilerinin de daha önce gördüklerini, ancak onu bir yıldız zannedip önem göstermediklerini anladılar. Bunlar içerisindeki en eski kayıtlar neredeyse 100 yıl öncesine, Flamsteed'in 1690 yılındaki gözlem kayıtlarına dayanıyordu.
Hemen keşiften sonra Newton kanunlarına dayanarak yapılan hesaplamalar ve gözlemlerin karşılaştırmasında Uranüs'ün yörüngesinde ters bir şeyler olduğu anlaşılmıştı. İkisi birbirine tam uymuyordu (yukarıdaki resimden bakarsak gezegenin yörüngesinde a-b yayını izlemesi gerektiği hesaplanmışken, gözlemlerde gezegenin a-c-b yayını izlediği görülüyordu). Problemi çözmeye çalışan astronomlar bunu bir türlü başaramayınca bazı opsiyonlar sundular: (1) acaba gezegen Güneş sisteminin uzak kesimlerinde bulunan bir çeşit değişik madde (gezegenin içinden geçtiği bir ortam) tarafından yavaşlatılıyor muydu? (2) Uranüs'ün yörüngesini bozan büyük bir uydusu mu vardı? ya da (3) keşfedildiği günden bu yana geçen sürede bir kuyrukluyıldız çarpması sonucu yörüngesi mi bozulmuştu?
Süregelen tartışmalar neticede olasılıkları iki seçeneğe kadar indirdi: ya Newton'un teorisi (ters kare kuralı) yanlıştı ya da Uranüs'ün yörüngesini etkileyen başka bir keşfedilmemiş gezegen söz konusuydu. Ünlü Fransız astronom Le Verrier'in Newton mekaniğine güveni sonsuzdu. Ona göre problemin cevabı başka bir gezegende yatmak zorundaydı. Varlığı bilinmeyen ama Uranüs'ün yörüngesini etkilediğini tahmin ettiği, Güneş'e Uranüs'ten daha uzakta yer alan bu 'hayali' gezegenin yörüngesini hesaplamaya girişti (Le Verrier böyle bir gezegenin olabileceğini öne süren ilk ya da tek kişi değildi).
Le Verrier bu hesaplamalarında bazı varsayımlarda bulunmak zorundaydı. İlk olarak bu hayali gezegenin yörüngesinin dairesel olmadığını kabul etti. İkinci olarak hayali gezegenin Uranüs'ten daha dışta olduğunu kabul etti. Son olarak da hayali gezegenin Uranüs'ün iki katı mesafede olduğunu varsaydı. Kendisinden önce yapılan gözlemlerle yeni gözlemleri birleştirdi. Sonunda 31 Ağustos 1846'da bir yazı yayımladı. Bu yazısında bu hayali gezegenin yörüngesine dair tüm detayları veriyordu. Le Verrier bilim tarihine geçen meşhur ifadeleriyle şöyle yazdı:
"Şimdi, kendini gökyüzünün belli bir bölgesini orada olması muhtemel bir gezegeni bulmak için bıkmadan tarayacak sabırlı bir gözlemci bulmak isterdim...Göreceksiniz ki, Uranüs'ün yörüngesindeki düzensizlikleri başka bir gezegen olmadan açıklamanın bir yolu yoktur ve bu gezegenin ekliptik üzerinde bu düzensizliklere yol açabilmesi için olabileceği tek bir yer vardır...Önümüzdeki bir kaç ay bu gezegeni bulabilmek için avantajlı bir konumdayız."
Bu sözler üzerinde daha bir ay geçmeden Galle, Eylül 1846'da bu gezegeni, yani Neptün'ü, Le Verrier'in verdiği tahmini koordinatlarda bulduğunu açıkladı. İşte olmuştu, Encke'nin Le Verrier'e yazdığı mektupta belirttiği üzere "evrensel kütle çekimi kanunun en makul kanıtı" bu şekilde bulunmuştu. Agnes Clerke'in dediği gibi "Newton kanunlarının mutlak kesinliği hakkında sahip olunan son şüpheler de böylece yok oldu".
Artık alışık olduğumuz üzere bu keşfin açıklanmasıyla kendi gözlem kayıtlarına bakan astronomlar aslında kendilerinin daha önceden Neptün'ü (tabi bir yıldız zannederek) kayıt altına aldıklarını farkettiler. Bu kayıtlar 1612-1613'te gözlem yapan Galileo'ya kadar gidiyordu. Yukarıdaki resimde Galileo'nun Neptün'ün Jüpiter ve aylarına kıyasla çizdiği konumunu ve altında aynı güne dair Stellarium programından aldığım konumları görebilirsiniz.
(5) Merkür'ün Yörüngesi
Merkür Güneş'e en yakın gezegen ve enteresan bir yörüngeye sahip. Yukarıdaki resimde görüldüğü üzere Güneş etrafında her bir tam turunda biraz kayan ve sonunda çiçeğe benzer bir desen oluşturan eliptik bir yörüngede dönüyor. Newton mekaniği Merkür'e uygulandığında görülüyor ki Merkür'ün günberi pozisyonu (yani Güneş'e en yakın olduğu pozisyon) her yılda bir 55.57 ark saniye kadar kaymalı. Ancak yapılan tüm gözlemler 56.00 ark saniyelik bir kayma gösteriyor. Yani teori ile gözlem arasında yüz yılda bir 43 ark saniye kadar bir uyuşmazlık söz konusu.
Neptün kaşifi Le Verrier, aynı yöntemle Merkür'ü ve yörüngesindeki aksaklıkları da incelemişti. Ününü borçlu olduğu Newton mekaniğine sonsuz güvenen Le Verrier, Uranüs'ün genişleyen yörüngesi probleminde olduğu gibi Merkür'ün düzensiz yörüngesinin de sebebinin henüz keşfedilmemiş bir gezegen olduğuna inanıyordu. Hesaplarına göre bu sefer bu düzensizliğe bir iç gezegen, yani Merkür'e kıyasla Güneş'e daha yakın bir gezegenin uyguladığı kütle çekimi kuvveti neden olmalıydı. Bu düşüncelerini açık ettikten sonra, Mart 1859'da aslen Fransız bir hekim olan amatör astronom Lescarbault, teleskobu ile Güneş'i gözlemlerken önünden küçük bir siyah daire yani bir gezegen silüetinin geçmekte olduğunu fark etti ve onu geçişini tamamlayana kadar uzunca bir süre takip etti ve zaman, lokasyon, açı vb. kayıtlarını not etti. Daha sonra bu bilgileri Le Verrier'e ulaştıran Lescarbault, Le Verrier tarafından tabi tutulduğu mülakat sonrasında Merkür'ün düzensizliklerinin sorumlusu olan bu Vulcan gezegeninin kaşifi olarak duyuruldu.
Sevinç içerisindeki Le Verrier, Lescarbault'un gözlem kaydına ve kendi hesaplarına dayanarak iç gezegen Vulcan'ın yörüngesine dair tüm detayları hızlıca hesaplayarak duyurdu. Bunları inceleyen diğer astronomlar yine, alışık olduğumuz üzere kendi geçmiş gözlem kayıtlarını incelediler ve en erken 1818 yılına ait kayıtlarda bu gözlemleri bulabildiler (Lloft'un gözlemleri). Keşfedilmesinden sonra da onu gözleyen bir çok astronom oldu ki bunlar Le Verrier'i son derece mutlu eden gözlemlerdi. Ancak şöyle bir problem vardı, Lescarbault'un gözlemleri sonrasında yaptığı hesaplarda Le Verrier, Vulcan'ın kütlesinin Merkür'ün kütlesinin en fazla on yedide biri olabileceğini belirtmişti. Bu durumda kütle çekim teorisine göre (ters kare ilişkisi) Merkür'ün yörüngesi üzerinde söz konusu etkiyi yapabilmesi için bir değil tam yirmi tane Vulcan olması gerekliydi. Kısacası Vulcan gözlenenden çok daha büyük olmalıydı. Tabi böyle olsa o güne kadar varlığının sır olarak kalması değil, çoktandır keşfedilmiş olması gerekirdi. Bu durum, bir şeylerin yanlış gittiğinin ilk ipuçlarından biriydi.
Vulcan'ı, Güneş'e yakın diğer gezegenleri de (Merkür ve Venüs) olduğu gibi gözlemlemenin en iyi yollarından birinin tam Güneş tutulmaları olduğunu bilen astronomi alemi 29 Temmuz 1878'de gerçekleşecek olan Güneş tutulmasını iple çekiyordu. Bu tutulma esnasında Vulcan tekrar görüldü ve önemli kayıtları yapıldı (Watson'un gözlemleri). Aslında Watson'un gözlediği gezegen de Merkür'ün düzensizliğine tek başına sebep olamayacak kadar küçüktü, ancak astronomlar arasında keşfedilmeyi bekleyen diğer gezegenlerin de aşikar olduğuna dair bir inanç vardı. Aynı şekilde Lewis Swift de tutulma sonrasında Vulcan'ı gözlemlediğini duyuranlar arasındaydı.
Bu tutulma aynı zamanda yavaş yavaş çatlak seslerin ve itirazların ortaya çıkmasına ön ayak oldu. Princeton'lu C. A. Young, Watson'un gözlemleri konusundaki şüphelerini dile getirmişti. Tam olarak aynı anda aynı yeri inceleyen diğer önemli astronomların gözlemlerine atıf yapan Young, bu astronomların hiç birinin Watson'un iddia ettiği yerde Vulcan'ı göremediğini belirtiyor ve Watson'un gözlemlerine kuşkuyla yaklaşıyordu. Watson ise Young'ı eleştirmişti: ona göre bu astronomların yaptığı "negatif kanıt sunarak keşfi engellemekti". Watson'a göre 'negatif kanıtlar' tamamen etkisizdi. Watson, tersine, Swift'in gözlemlerine atıf yaparak onun gözlemleriyle kendininkileri destekliyordu. Kendini Young ve diğerlerine karşı savunurken şöyle diyordu: "Onların gösterdiği yerlerde bilinen yıldızlar yer almıyor, dolayısıyla gözlemlediğim cismin kimliğine dair yanılıyor olamam". Ancak, sonunda Swift ve Watson'un aslında farklı cisimleri gördükleri ortaya çıkacaktı.
Vulcan takip eden 1880, 1882 ve 1883 Güneş tutulmalarında da aranmaya devam edildi. Yine astronomlar tarafından bir kaç kez görüldüğü duyuruldu. Hatta bazıları Vulcan benzeri birden fazla iç gezegen gördüğünü de açıkladı. Ancak, tüm bunlar boşunaydı. Merkür'ün günberi pozisyonunun açıklanamayan değişimi hala çözümsüzdü. Teori ve hesaplar birbirini halen tutmuyordu. En çok inanıldığı günlerde bile Vulcan aslında bu problemin çözümüne çok ufak bir katkıdan fazlasını (küçük kütlesi nedeniyle) yapamıyordu. Newton'un teorisine göre Vulcan'ın en azından Merkür ile eş kütlede olması gerekirdi. 1880'lerden sonra astronomlar yavaş yavaş Vulcan'a dair inançlarını yitirmeye başladılar ve zamanla tamamen kaybettiler.
Albert Einstein ve Genel Görelilik Teorisi
1905 yılında (annus mirabilis) uzay-zamanın yapısıyla ilgili Özel Görelilik Teorisini yayımlayan Einstein, 1915'e geldiğimizde ise uzun bir süredir bir çeşit kütle çekim teorisi olan Genel Görelilik Teorisi üzerinde çalışıyordu ve aynı yıl bu konudaki meşhur makalesini yayımlayarak Vulcan'ı, defalarca kez gözlemlenen, ancak son zamanlarda varlığına dair umutların azaldığı hayali gezegeni, çalışma masasından yok etmeyi başarmıştı. Bunu, o güne kadar ki tüm zorlu sınamalardan başarıyla çıkan Newton mekaniğini (ve kütle çekim teorisini) çürüterek yapmıştı. Evet, Vulcan veya Vulcan'a benzer gezegenler yoktu ve teori ile hesaplamaların uyuşmamasının bu seferki sebebi hatalı hesaplamalar değil, bu hesapların dayandığı teorinin yanlış olmasıydı. Artık Newton'un teorisinin yerini Einstein'ınki almalıydı. Peki Einstein'ın Genel Görelelik Teorisi neydi, ne diyordu?
Öncelikle, Einstein direkt olarak ve yalnızca Merkür'ü incelemiyordu. O, Merkür'ün yörüngesine dair problemin farkındaydı, ancak bu problemi çözmekten daha fazlası peşindeydi. O genel bir teorinin ardından koşuyor ve kendi teorisinin doğruluğunu Merkür problemi üzerinde test etmek istiyordu. Onun yeni kütle çekim teorisini içeren Genel Görelilik Teorisine göre uzaydaki objeler kütleleriyle orantılı olarak uzay-zamanda eğilip bükülmelere neden oluyordu ve uzayın geometrisinde oluşan bu bozulma netice olarak kütle çekimine yol açıyordu (Newton ise varlığının farkında olsa ve formülasyonunu yapmış olsa da hiç bir zaman kütle çekimin sebebini açıklayamadı). Yani, kütle çekimi, dev kütlelerin direkt olarak uyguladığı görünmez ve gizemli bir kuvvet değil, uzayın geometrisi ile ilgili bir durumdu. Einstein'a göre bu bükülmeler ya da bozulmalar Dünya gibi görece küçük nesneler için daha küçük olurken Güneş gibi devasa cisimler için ise çevresindeki diğer cisimlerin yörüngelerini etkileyecek kadar büyük olabiliyordu (alttaki resim). Einstein daha sonra, uzay-zamanın maddeye nasıl hareket etmesi gerektiğini ve maddenin de uzay-zamana nasıl bükülmesi gerektiğini söylediği bu düşüncesinin 'yaşamının en mutlu düşüncesi' olduğunu söyleyecekti.
Düşünce güzel ve mutlu olsa da kanıtlanmaya (daha doğrusu sınamalardan başarıyla çıkmaya) muhtaçtı. Merkür'ün yörüngesine dair meşhur problem bu yeni teoriyi test etmek için biçilmiş kaftandı. Einstein, Öklidyen olmayan bu geometride (bükülmüş uzay) doğru hesaplamaları yapabilmek için dönemin matematikçilerinden (Schwarzschild) destek aldıktan sonra kendi teorisine göre Güneş etrafındaki uzay-zamanda tam olarak ne gibi bir bükülme olduğunu hesaplayarak bunun Merkür'ün yörüngesi üzerinde ne gibi bir etkisi olabileceğini incelemeye başladı. Hesaplarına göre bu bükülmenin Newton mekaniğiyle yapılan hesaba göre Merkür üzerinde hızlandırıcı bir etkisi olacağı belliydi.
Einstein, gerekli tüm çalışmayı yaptıktan sonra, kendi ifadesiyle heyecan ve mutluluktan kalbinin çarpıntılarını duyduğu için çalışamadığı üç gün geçirmesine neden olacak keşfini yaptı: uzay-zamanın Güneş'in kütlesi nedeniyle bükülmesi durumunda Merkür'ün yörüngesinde gerçekleşecek olan değişim (Newton mekaniğine kıyasla) tam olarak yüz yılda 43 ark saniye kadardı. Bu sayı daha önce belirttiğim gözlem sonuçlarıyla birebir uyuyordu. İşte olmuştu. Teori ve gözlem uyuşmamış ve bu sefer var olan teori başaramamış ve yerine yeni bir teori gelmişti. Einstein'ın teorisi diğer tüm gezegenler için de tutuyordu. Güneş'in dev kütlesinden uzaklaştıkça uzay-zaman bükülmesi de azaldığı için Newton'un teorisi ile aynı sonucu verse de, Newton mekaniği Güneş'e yaklaştıkça geçersiz olmaya başlıyordu.
Einstein'ın, Merkür'ün yörüngesinin günberi problemini çözmesi Genel Görelilik Teorisi'nin ilk ve en önemli zaferlerinden biriydi. Daha sonra Venüs'ün yörüngesindeki düzensizlikleri de, bir çok farklı problemi de (1975'te Güneş sistemi dışındaki bir çift yıldız sistemine uygulandığında da yine geçerli olduğu görülmüştü) aynı şekilde açıklamak mümkün olmuştu. Teorinin en büyük kanıtlarından biri ise hemen dört yıl sonrasında, 1919 senesindeki Güneş tutulmasında Eddington tarafından elde edilmişti. Eddington tutulma sırasında Dünya'dan bakıldığında izdüşümsel konumu Güneş'e yakın olan bazı yıldızları gözlemlemiş ve bunlardan gelen fotonların Güneş'in yakınından geçip bizim gözümüze ulaşırken nasıl da Güneş etrafındaki uzay-zaman bükülmesinden etkilenerek aslında olmaları gereken yerde değil de daha farklı bir pozisyonda göründüklerini gözlemlemeyi başarabilmişti.
Cevapsız Kalan Sorular
Gazetelere konu olan bu deney sonrasında Einstein da teorisi gibi dünya çapında bir üne kavuşmuştu. Artık sorularımızı yanıtlayan yeni bir teorimiz vardı ve Vulcan veya Vulcanlara ihtiyacımız kalmamıştı. Ancak yine de, geride bazı ilginç sorular cevapsız kalmıştı. En önemlisi, Lescarbault 1859'da Vulcan'ı görmediyse ne görmüştü ve uzunca bir süre izleyip kaydını tutmuştu? Lescarbault bir amatördü ve muhtemelen basitçe bir hata yapmıştı. Peki ya Watson ve Swift? Bunlar tanınmış, becerikli ve ömrünü gökyüzüne ve gök cisimlerine adamış astronomlardı ve gözlem yapmayı iyi biliyorlardı. Onlar muhtemelen gerçekten bir şey görmüşlerdi. Bunun ne olduğunu ise bilmenin bir yolu yok. Belki bilinen cisimlerden birini gördüler, belki bir asteroid, belki de bir kuyrukluyıldız. Öte yandan Vulcan'ı gördüğünü açıklayan bir çok başka astronom da vardı. Bu kadar insanın aynı hatayı yapması nasıl mümkün olmuştu? Var olmayan bir gezegen nasıl olmuş da zamanının Güneş sistemi haritalarına girmeyi başarmıştı, herkes varlığından bu kadar emin olabilmişti? Belki de Newton kanunlarına olan sonsuz inançları yüzünden Vulcan'a dair beklentileri onları yanıltmıştı ve görmek istedikleri şeyi gördüklerini düşündürtmüştü.
Sahi, en başta da dediğimiz gibi, bir şey hiç var olmamışsa kaybolabilir miydi, yoksa önce bulunması mı gerekirdi? Peki, daha önemlisi, olmayan bir şey nerede bulunurdu? Unutmayın evin anahtarından değil, Güneş sistemimizdeki koca bir gezegenden bahsediyoruz...Belki Vulcan'ın bir hayal olduğu ortaya çıkacaktı, ama O bizi nihayetinde doğrulara ulaştıran bir hayaldi. Sonunda herkese gösterecekti ki, koca bir gezegen bile insanlığın kümülatif beklentilerinden büyük olamazdı ve yine de hiç bir yanlış inancın gerçeğin karşısında sonsuza dek sağlam durması mümkün değildi.
Başlıca Kaynaklar:
1. The Ghost in Newton's Clockwork Universe - In Search of Planet Vulcan, Richard Baum & William Sheehan, 1997, Springer.
2. The Hunt for Vulcan: How Albert Einstein Destroyed a Planet and Deciphered the Universe, Thomas Levenson, 2015,
3. Feynman'ın Kayıp Dersi, Gezegenlerin Güneş Çevresindeki Hareketi, Goodstein ve Goodstein, 2003
4. Inside Einsteins Mind The Enigma of Space and Time, BBC
5. https://aether.lbl.gov/www/classes/p10/gr/PrecessionperihelionMercury.htm
6. https://www.nationalgeographic.com/news/2015/11/151104-newton-einstein-gravity-vulcan-planets-mercury-astronomy-theory-of-relativity-ngbooktalk/
1859 yılında varlığını bildiğimiz gezegenlere şöyle bir bakalım: Güneş'e en yakından başlarsak altı gezegen, yani Merkür, Venüs, Dünya, Mars, Jüpiter ve Satürn zaten antik zamandan beri biliniyordu (Dünya'nın yaklaşık iki bin sene kadar gezegen kabul edilmediğini biliyoruz, ancak bu başka bir yazının konusu). Teleskoptan sonraki dönemde ise iki gezegen, 1781'de Uranüs ve 1846'da Neptün, bulunmuştu. Dolayısıyla sekiz gezegen cepteydi. 2006'nın ikinci yarısında Uluslararası Astronomi Birliğinin kararıyla gezegenlik statüsünden çıkarılan Pluton'u da eklersek dokuzu tamamlıyoruz, peki bunun neresi ilginç? Şurası: Pluton 1859'da henüz keşfedilmemişti ve bir yetmiş yıl daha keşfedilemeyecekti. Öyleyse, dokuzuncu gezegen eğer Pluton değilse hangisiydi ve şu an nerede?
Bu yazıda bilim tarihindeki en enteresan anekdotlardan biri olan kayıp gezegen Vulcan'ın hikayesini anlatacağım. Sahi bir şey hiç var olmamışsa kaybolabilir mi, yoksa önce bulunması mı gerekir? Peki olmayan bir şey nasıl bulunur? Unutmayın evin anahtarından değil, güneş sistemimizdeki koca bir gezegenden bahsediyoruz, bunlar sormaya pek de alışık olduğumuz sorular değil.
Vulcan, Güneş sistemimizde Merkür ve Güneş arasında yer alan, zamanında herkesin varlığına inandığı, astronomların gözlediği, gazetelerin ise haberlerini yaptığı, ancak aslında hiç var olmamış bir gezegendi. İsmini Güneş'e olan yakınlığından dolayı Roma mitolojisindeki Ateş Tanrısından almıştı. Bu sıcak gezegen 26 Mart 1859'da Fransız amatör astronom Edmond Modeste Lescarbault tarafından keşfedilmişti.
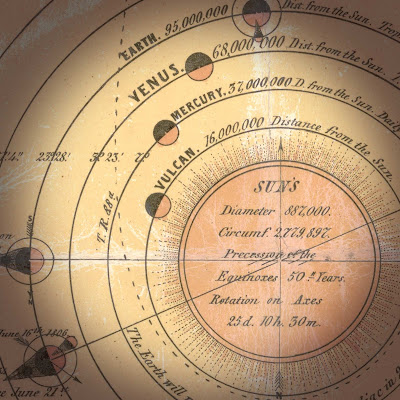 |
| 18.yy sonu güneş sistemimiz, Merkür ve Güneş arasına dikkat edin (Kaynak: Library of Congress) |
Lescarbault'un gözlemlerinde aldığı notlardan, daha sonra zamanın ünlü Fransız astronomu Le Verrier tarafından hesaplandığı üzere, Vulcan Güneş'ten 0.147 AU mesafedeydi ve Güneş etrafındaki bir turu 19 gün 17 saat sürüyordu. Yörüngesi ekliptiğe göre 12 derece 10 dakika kadar eğikti. Daha önce görülmediğine göre Merkür'den daha karanlık bir gezegen olmalıydı. Vulcan her sene 3 Nisan ile 6 Ekim arasında Güneş'in önünden en az iki, genellikle ise dört kez geçmeliydi. Tüm bu teknik detaylara ve hesaplamalara bakılırsa Vulcan hakkında bilmediğimiz bir şey yok gibiydi. Üstelik, Le Verrier'in, Lescarbault'un gözlemlerine dayanarak yaptığı bu açıklamalar sonrasında bir çok tanınmış ve güvenilir astronom kendi gözlem notlarına bakarak bu gezegeni aslında Lescarbault'tan daha önce görmüş ve defterlerine kaydetmiş olduklarını fark ettiler ve bunu açıkça beyan ettiler. Tek problemse Vulcan diye bir gezegenin hiç bir zaman var olmamış olmasıydı. Peki tüm bunların açıklaması neydi? Bu açıklamayı yapmamız için biraz eskiye, Kepler ve Newton zamanlarına gitmemiz ve tarihte yavaş yavaş ilerlememiz gerekiyor.
Kepler ve Newton
Kepler'in (1571-1630) gezegenlerin hareketine dair üç yasası şöyle özetlenebilir: (1) tüm gezegenlerin yörüngeleri, bir odağında Güneş olan elipslerdir, (2) Güneş'ten gezegene uzanan bir çizgi, eşit zamanlarda eşit alanlar süpürür ve (3) tüm gezegenlerin yörüngelerindeki bir turu için geçen sürenin karesi ile elipsin merkezine olan mesafenin küpü aynıdır.
 | |
|
Kepler'in bu üç yasasının bilmemiz gereken önemli bir özelliği var: bu üç yasa tamamen ve yalnızca gözlemlere dayanıyor. Peki bu tam olarak ne anlama geliyor? Kısacası, Kepler gökyüzüne bakmış, incelemiş, notlar almış, gezegenlerin ne zaman nerede göründüklerini kaydetmiş ve en sonunda bunları bir eğri üzerine oturttuğunda yörüngelerinin bir elipsi oluşturduğunu görmüştü. Tabi Kepler'in bunları yaparken zamanının en iyi gözlemlerini yapan meşhur astronomu Danimarkalı Tycho Brahe (astronomi merkezi Uraniborg'un kurucusu ve yöneticisi) ile çalıştığını ve bu sayede eline son derece keskin, kesin ve hassas ölçümler sonucu oluşturulmuş verilerin geçtiğini bilmemiz gerekir. Aynı şekilde, Kepler'in 2. ve 3. yasaları da bu şekilde gökyüzü gözlemlerinden yapılan genellemelerden ibaretti ve elindeki verileri nasıl formüle edebileceğini araştırarak bu sonuçlara ulaşabilmişti. Örneğin (2) no'lu yasanın geçerli olması için gezegenlerin Güneş'e yakınken hızlı ve Güneş'ten uzakken daha yavaş hareket ettiğini fark etmesi doğal olarak gerçekleşiyordu zaten. Aynı şekilde gezegenlerin periyotlarını ve Güneş'e olan mesafelerini irdelediğinde tüm gezegenlerde bunların belli derecelerden oranlarının aynı olduğunu fark etmişti (3. yasa). Burada dikkat etmemiz gereken husus şu: Kepler gezegenlerin yörüngesinin elips olduğunu söylemişti, ama onun neden elips olduğu üzerine ya da nasıl bir sistemde eliptik bir yörünge oluşacağı üzerine bir şey söyleyememişti. Bunun için Newton'u beklememiz gerekecekti.
 |
| Newton'un Principia'sı ve burada yazdığı harekete dair 3 kanunu |
Newton'un harekete dair kanunları ile Kepler'inkiler doğaları açısından birbirlerinden çok ayrıdır. Kepler yalnızca noktaları birleştirmiş, gözlemsel sonuçlara varmıştı ve söyledikleri yalnızca gezegenlerin hareketi için geçerliydi çünkü gözlemleri orayla sınırlıydı. Newton'un kanunları ise doğanın fiziksel yapısı hakkında hipotezlerdi ve basit gözlemlerden (Kepler'in yaptığı da tabi ki çok değerli) çok fazlasıydı. Üstelik bunlar yalnızca gezegenlerin hareketleriyle sınırlı olmayıp onlar da dahil olmak üzere her türlü hareket için geçerli olma iddiasındaki evrensel kurallardı. Newton'un kanunlarının (ya da hipotezlerinin) sınanmaya ihtiyacı vardı. Geçerlilikleri, test edilmelerine, çürütülmeye çalışılmalarına ve en sonunda tüm bu testleri başarıyla atlatabilmelerine bağlıydı. Yani Popper'ın 'falsification' dediği bilimin yanlışlanabilir olma özelliğine (ve aslında Popper'dan daha önce Einstein'ın 'Induction and Deduction in Physics' isimli makalesinde yazdığı gibi "bir teorinin doğruluğu asla kanıtlanamaz" ancak yanlışlığı gösterilebilir, ilkesine.)...
Newton Mekaniği ve Önemli Sınamalar
Newton'un harekete dair bu meşhur kanunları tarihte önemli sınamalardan geçti. Bu yazıda bunlardan beş tanesine bakacağız: (1) Ay Problemi (2) Halley Kuyrukluyıldızı'nın Yörüngesi (3) Jüpiter ve Satürn Eşitsizliği (4) Uranüs'ün Genişleyen Yörüngesi (5) Merkür'ün Yörünge Kayması
(1) Ay Problemi
 |
| Ay'ın Dünya çevresindeki hareketi (Kaynak: https://wisp.physics.wisc.edu/) |
Ay Problemi 1749'da, ancak Newton öldükten yirmi yıl kadar sonra çözülebildi. Problem şuydu: Bugüne kadarki gözlemlere göre, Ay'ın Dünya çevresinde takip ettiği yörüngeye baktığımızda Dünya'ya en yakın ve en uzak olduğu noktaları birleştiren doğru (yani yukarıdaki resimdeki 'Line of Apsides') her ay Ay'ın döndüğü yönde 3° 23' ilerlemekteydi. Newton ise 'matematiğe' yani kendi teorisine göre hesapladığında bunun 1° 31' 14'' olması gerektiğini görmüştü (Kepler'den farkı burada, Newton bir sistem kurup buna göre ne olması gerektiğini hesaplıyor, Kepler ise gözlem yapıp sonucunda gözlemlerinin uyduğu formülü açıklıyor). Yani teori ve gözlem uyuşmuyor.
Euler 1747'de "Ay'a etkiyen kuvvetlerin Netwon'un kurallarına uymadığını gösteren bir çok kanıt sunabilirim" dediğinde işte bu durumu kastediyordu. Aynı şekilde Clairaut, Newton'un kurallarının yanlış olduğuna atıf yaparak ters kare kuralının terk edilmesi gerektiğini belirtiyordu. Peki Newton gerçekten hatalı mıydı? Newton mekaniği yanlış mıydı? Gözlemler ve teori neden birbirini tutmuyordu?
Newton bu problemi çözmeye çalışırken, bize lisede ve örgün öğretimin çeşitli aşamalarında da öğretildiği gibi bazı varsayımlar yapıyordu. Örneğin, nasıl ki biz problemlerde pi'yi bazen iki basamağına kadar alırız, yuvarlarız ya da bazen çok küçük bazı değerlerin etkisini sonuca anlamlı etkisi olmayacağı ve hesabı çok zorlaştıracağı için 'ihmal edilebilir' diyerek göz ardı ederiz, aynı şekilde Newton da Ay'ın yörüngesini kendi kanunları kapsamında hesaplarken bazı varsayımlarda bulunmuştu. Hesaplarında, Ay'ın Dünya'ya göre relatif hareketi Güneş ile kıyaslandığında çok daha hızlı olduğu için Güneş'in pozisyonunu 'uzakta sabit bir nokta' olarak almıştı. Ancak sonrasında (görmeye kendi ömrü vefa etmese de) aslında Güneş'in hareketinin ihmal edilebilir olmadığı ortaya çıkmıştı.
Bu problemi 1749'da çözen Clairaut, Güneş'in pozisyonunu sabit olarak almadan Newton mekaniğine dayalı kapsamlı bir analize girişmişti. Newton kurallarından sapmadan, bu şekilde yaptığı hesaplamaları sonucunda görmüştü ki Ay Dünya'dan en uzak noktadayken Güneş'in hareketi ile aynı yönde olduğu için 'line of apsides' ilerlemekte, Ay Dünya'ya en yakındayken ise Güneş'in hareketi ters yönde olduğu için gerilemekteydi. Oluşan bu eşitsizlik sonucunda daha çok eşitsizlik oluşuyor ve bu ikincil dereceli etkiler toplandığında gözlem sonucu ile hesaplama sonucu birbirini sonunda tutuyordu. Yani hatalı olan Newton mekaniği değil, hesaplamalar yapılırken 'ihmal edilebilir' diye sınıflandırılan, ama aslında 'ihmal edilemeyecek olan' bir takım varsayımlardı.
Ay problem çözülmüştü. Astronom Robert Grant'ın özetlediği gibi "Newton'un teorisini tamamen çökertebilecek bu problem sonunda onun doğruluğunun en büyük göstergelerinden biri olarak sonuçlanmıştı".
(2) Halley Kuyrukluyıldızı'nın Yörüngesi
 |
| Gezegenler ve Halley (Kaynak: nasa.gov) |
Sivri eliptik yörüngesi nedeniyle Güneş Çevresindeki hareketinde Neptün'den bile uzaklara ulaşan (resimdeki kırmızı rota) Halley Kuyrukluyıldızı Dünya'dan yaklaşık her 75 yılda bir çıplak gözle görülebiliyor. İlk kayıtları Çin'de M.Ö. 239 civarında tutulan Halley o zamandan bu yana defalarca kez bizi ziyaret etti, etmeye de devam ediyor. Astronomlar uzun süreler bu kuyrukluyıldızın yörüngesini hesaplamaya ve tam olarak ne zaman geri geleceğini tahmin etmeye çalıştılar.
Newton sonrası yakın geçmişe baktığımızda, Ay problemini çözen Clairaut da Halley'in ne zaman döneceğini hesaplamaya çalışanlardandı. Daha önce 1531, 1607, 1682'de geldiğini ve günberi (Güneşe en yakın olduğu konum) pozisyonuna ulaştığını biliyordu. Yani her geldiğinde tam aynı olmasa da yaklaşık 75 ya da 76 senelik bir periyotu var gibiydi. Ancak tam olarak hangi ayın hangi günü geleceğini ve günberiye ulaşacağını kestirmek henüz mümkün olmamıştı ve astronomlar arasında bu popüler ve çözene prestij kazandıracak bir problemdi.
Newton'un çağdaşı, Principia'nın yayımcısı ve kendisinin az sayıdaki arkadaşlarından biri olan Edmond Halley (bu kuyrukluyıldıza ismi verilen şahıs), Halley'in 1682'de günberiye ulaşmadan önce 1681'de Jüpiter'e fazlaca yaklaştığını fark etmişti. Kuyrukluyıldız, Jüpiter'in kütle çekiminden etkilenmiş ve yörüngesi bir miktar genişlemek zorunda kalmıştı. Dolayısıyla bir sonraki gelişinin gecikmesi beklenen bir şeydi. Ama ne kadar? Halley, 1758'in sonu ya da sonraki senenin başında geleceğini tahmin etmişti.
Ay probleminden tecrübeyle bazı hesaplamalarda ihmal edilebilir görülen şeylerin aslında nasıl ihmal edilemez olduğunun farkında olan Clairaut ise kuyrukluyıldızın yörüngesinde bir kaç gün arayla pozisyonlarının ve her pozisyonda Jüpiter ve Satürn gibi dev gezegenlerden mesafesinin hesaplanması gerektiğini ve bu şekilde bunların yörünge üzerindeki etkisinin görülebilieceğini düşünüyordu. Hesaplamanın doğru sonuç vermesi için Jüpiter ve Satürn'ün etkisinin tüm yörünge üzerine yedirilmesi gerekliydi. Hatta, Jüpiter'in Güneş'e uyguladığı çekim kuvveti bile 'ihmal edilmemeliydi'. Çünkü Güneş'in pozisyonundaki en ufak bir değişiklik bile kuyrukluyıldızın yörüngesinde anlamlı bir fark yaratabilirdi.
Clairaut, Newton mekaniğine dayanan kapsamlı hesaplamaları neticesinde Halley'in 1759 Nisan ayı ortası civarında (+/- 1 ay toleransla) günberiye ulaşacağını açıkladı. Bir aylık tolerans aslında 1682 yılındaki gözlem kayıtlarındaki olası hatalara dayanıyordu. Clairaut'un ve dayandığı Newton kanunlarının doğruluğu bir kez daha, Halley'in 13 Mart 1759'da günberiye ulaşmasıyla desteklenmiş oldu. Bir kez daha gözlemler ile teori birbiriyle uyuşmuştu. Evrensel kütle çekimi teorisi bir kez daha başarmıştı (kanıtlanmış oldu diyemiyoruz, çünkü bir teori ancak çürütülebilir, fakat kanıtlanamaz - ama desteklenebilir).
(3) Jüpiter ve Satürn Eşitsizliği
 |
| Her 20 yılda bir yaklaşan Jüpiter ve Saturn ile her 60 yılda bir başa dönen döngü (mavi daireler içinde Jüpiter ve Satürn) |
Jüpiter ve Satürn'ün yörüngelerinde Newton kanunlarına dayanan hesaplamalara bakıldığında yanlış bir şeyler vardı. Antik ve modern gözlemlere bakıldığında Jüpiter yavaş, Satürn ise olması gerekenden hızlı görünüyordu. Astronomları düşündüren bu problem Newton'dan sonra 1700'lerin sonuna kadar henüz çözülmüş durumda değildi. Aslında, bu problemin kaynağı gezegenlerin birbirleri üzerindeki çekim kuvvetlerinin uzun vadelerde yörüngelerinde yarattığı düzensizliklerdi. Tüm 17. yüzyıl boyunca Satürn'ün periyotu artmış ve Jüpiter'inki ise kısalmıştı. Satürn devamlı olarak hesaplanan yörüngesinden geride kalıyordu. Jüpiter ise kendi hesaplı yörüngesinden önde gidiyordu. Öte yandan tüm 18. yüzyıl boyunca ise bunun tam tersi olmaktaydı.
Problemi 1784'te yine Newton mekaniği ile çözen Laplace oldu. Açıklaması şöyleydi: Jüpiter'in Güneş çevresindeki hareketinin periyotunun 5 katı Satürn'ün periyotunun 2 katıyla denk durumdaydı (bunu Kepler'in 3. kanunu ile de basitçe hesaplayabiliriz). Bu demek oluyor ki Jüpiter (1 yılı Dünya'nın ~12 yılına eşit) ve Satürn (1 yılı Dünya'nın ~30 yılına eşit) her 5 Jüpiter yılı ve 2 Satürn yılı sonrasında yani bizim dilimizle 60 yılda bir döngülerinde aynı çizgi üzerinde buluşuyorlardı. Bu buluşmanın ve yakınlaşmanın kütle çekim anlamında kümülatif etkisi ise Laplace'ın Newton kanunları ile hesapladığı üzere, yörüngelerde gözlemlenen oldukça büyük bir düzensizlik oluyordu. Böylece, bir kez daha uzun zamandır bilinen bir problem, Newton mekaniği ile çözülmüş oluyordu.
(4) Uranüs'ün Genişleyen Yörüngesi
 |
| Uranüs'ün yörüngesindeki sapma |
18. yüzyıl sonlarında, zamanının ünlü astronomu Herschel tüm gökyüzünü sistematik bir şekilde tarayarak her şeyi not etmeye ve gökyüzünün tam bir haritasını oluşturmaya karar vermişti. Bu çabalarının neticesinde 1781 yılında daha önce farkında olmadığımız bir gezegeni, yani bugünkü Uranüs'ü bulmuştu. Herschel'in bu keşfi neticesinde kendi gözlem kayıtlarına bakan bazı astronomlar Uranüs'ü kendilerinin de daha önce gördüklerini, ancak onu bir yıldız zannedip önem göstermediklerini anladılar. Bunlar içerisindeki en eski kayıtlar neredeyse 100 yıl öncesine, Flamsteed'in 1690 yılındaki gözlem kayıtlarına dayanıyordu.
Hemen keşiften sonra Newton kanunlarına dayanarak yapılan hesaplamalar ve gözlemlerin karşılaştırmasında Uranüs'ün yörüngesinde ters bir şeyler olduğu anlaşılmıştı. İkisi birbirine tam uymuyordu (yukarıdaki resimden bakarsak gezegenin yörüngesinde a-b yayını izlemesi gerektiği hesaplanmışken, gözlemlerde gezegenin a-c-b yayını izlediği görülüyordu). Problemi çözmeye çalışan astronomlar bunu bir türlü başaramayınca bazı opsiyonlar sundular: (1) acaba gezegen Güneş sisteminin uzak kesimlerinde bulunan bir çeşit değişik madde (gezegenin içinden geçtiği bir ortam) tarafından yavaşlatılıyor muydu? (2) Uranüs'ün yörüngesini bozan büyük bir uydusu mu vardı? ya da (3) keşfedildiği günden bu yana geçen sürede bir kuyrukluyıldız çarpması sonucu yörüngesi mi bozulmuştu?
Süregelen tartışmalar neticede olasılıkları iki seçeneğe kadar indirdi: ya Newton'un teorisi (ters kare kuralı) yanlıştı ya da Uranüs'ün yörüngesini etkileyen başka bir keşfedilmemiş gezegen söz konusuydu. Ünlü Fransız astronom Le Verrier'in Newton mekaniğine güveni sonsuzdu. Ona göre problemin cevabı başka bir gezegende yatmak zorundaydı. Varlığı bilinmeyen ama Uranüs'ün yörüngesini etkilediğini tahmin ettiği, Güneş'e Uranüs'ten daha uzakta yer alan bu 'hayali' gezegenin yörüngesini hesaplamaya girişti (Le Verrier böyle bir gezegenin olabileceğini öne süren ilk ya da tek kişi değildi).
 |
| Fransız astronom Le Verrier (Kaynak: https://colnect.com/) |
Le Verrier bu hesaplamalarında bazı varsayımlarda bulunmak zorundaydı. İlk olarak bu hayali gezegenin yörüngesinin dairesel olmadığını kabul etti. İkinci olarak hayali gezegenin Uranüs'ten daha dışta olduğunu kabul etti. Son olarak da hayali gezegenin Uranüs'ün iki katı mesafede olduğunu varsaydı. Kendisinden önce yapılan gözlemlerle yeni gözlemleri birleştirdi. Sonunda 31 Ağustos 1846'da bir yazı yayımladı. Bu yazısında bu hayali gezegenin yörüngesine dair tüm detayları veriyordu. Le Verrier bilim tarihine geçen meşhur ifadeleriyle şöyle yazdı:
"Şimdi, kendini gökyüzünün belli bir bölgesini orada olması muhtemel bir gezegeni bulmak için bıkmadan tarayacak sabırlı bir gözlemci bulmak isterdim...Göreceksiniz ki, Uranüs'ün yörüngesindeki düzensizlikleri başka bir gezegen olmadan açıklamanın bir yolu yoktur ve bu gezegenin ekliptik üzerinde bu düzensizliklere yol açabilmesi için olabileceği tek bir yer vardır...Önümüzdeki bir kaç ay bu gezegeni bulabilmek için avantajlı bir konumdayız."
Bu sözler üzerinde daha bir ay geçmeden Galle, Eylül 1846'da bu gezegeni, yani Neptün'ü, Le Verrier'in verdiği tahmini koordinatlarda bulduğunu açıkladı. İşte olmuştu, Encke'nin Le Verrier'e yazdığı mektupta belirttiği üzere "evrensel kütle çekimi kanunun en makul kanıtı" bu şekilde bulunmuştu. Agnes Clerke'in dediği gibi "Newton kanunlarının mutlak kesinliği hakkında sahip olunan son şüpheler de böylece yok oldu".
 |
| Galileo'nun gözlemlerindeki Neptün çizimi ve Stellarium'dan uygulamasından aynı güne ait simulasyon sonucu |
Artık alışık olduğumuz üzere bu keşfin açıklanmasıyla kendi gözlem kayıtlarına bakan astronomlar aslında kendilerinin daha önceden Neptün'ü (tabi bir yıldız zannederek) kayıt altına aldıklarını farkettiler. Bu kayıtlar 1612-1613'te gözlem yapan Galileo'ya kadar gidiyordu. Yukarıdaki resimde Galileo'nun Neptün'ün Jüpiter ve aylarına kıyasla çizdiği konumunu ve altında aynı güne dair Stellarium programından aldığım konumları görebilirsiniz.
(5) Merkür'ün Yörüngesi
 |
| Merkür'ün Güneş Etrafındaki Hareketi (Kaynak: https://aether.lbl.gov/) |
Merkür Güneş'e en yakın gezegen ve enteresan bir yörüngeye sahip. Yukarıdaki resimde görüldüğü üzere Güneş etrafında her bir tam turunda biraz kayan ve sonunda çiçeğe benzer bir desen oluşturan eliptik bir yörüngede dönüyor. Newton mekaniği Merkür'e uygulandığında görülüyor ki Merkür'ün günberi pozisyonu (yani Güneş'e en yakın olduğu pozisyon) her yılda bir 55.57 ark saniye kadar kaymalı. Ancak yapılan tüm gözlemler 56.00 ark saniyelik bir kayma gösteriyor. Yani teori ile gözlem arasında yüz yılda bir 43 ark saniye kadar bir uyuşmazlık söz konusu.
Neptün kaşifi Le Verrier, aynı yöntemle Merkür'ü ve yörüngesindeki aksaklıkları da incelemişti. Ününü borçlu olduğu Newton mekaniğine sonsuz güvenen Le Verrier, Uranüs'ün genişleyen yörüngesi probleminde olduğu gibi Merkür'ün düzensiz yörüngesinin de sebebinin henüz keşfedilmemiş bir gezegen olduğuna inanıyordu. Hesaplarına göre bu sefer bu düzensizliğe bir iç gezegen, yani Merkür'e kıyasla Güneş'e daha yakın bir gezegenin uyguladığı kütle çekimi kuvveti neden olmalıydı. Bu düşüncelerini açık ettikten sonra, Mart 1859'da aslen Fransız bir hekim olan amatör astronom Lescarbault, teleskobu ile Güneş'i gözlemlerken önünden küçük bir siyah daire yani bir gezegen silüetinin geçmekte olduğunu fark etti ve onu geçişini tamamlayana kadar uzunca bir süre takip etti ve zaman, lokasyon, açı vb. kayıtlarını not etti. Daha sonra bu bilgileri Le Verrier'e ulaştıran Lescarbault, Le Verrier tarafından tabi tutulduğu mülakat sonrasında Merkür'ün düzensizliklerinin sorumlusu olan bu Vulcan gezegeninin kaşifi olarak duyuruldu.
Sevinç içerisindeki Le Verrier, Lescarbault'un gözlem kaydına ve kendi hesaplarına dayanarak iç gezegen Vulcan'ın yörüngesine dair tüm detayları hızlıca hesaplayarak duyurdu. Bunları inceleyen diğer astronomlar yine, alışık olduğumuz üzere kendi geçmiş gözlem kayıtlarını incelediler ve en erken 1818 yılına ait kayıtlarda bu gözlemleri bulabildiler (Lloft'un gözlemleri). Keşfedilmesinden sonra da onu gözleyen bir çok astronom oldu ki bunlar Le Verrier'i son derece mutlu eden gözlemlerdi. Ancak şöyle bir problem vardı, Lescarbault'un gözlemleri sonrasında yaptığı hesaplarda Le Verrier, Vulcan'ın kütlesinin Merkür'ün kütlesinin en fazla on yedide biri olabileceğini belirtmişti. Bu durumda kütle çekim teorisine göre (ters kare ilişkisi) Merkür'ün yörüngesi üzerinde söz konusu etkiyi yapabilmesi için bir değil tam yirmi tane Vulcan olması gerekliydi. Kısacası Vulcan gözlenenden çok daha büyük olmalıydı. Tabi böyle olsa o güne kadar varlığının sır olarak kalması değil, çoktandır keşfedilmiş olması gerekirdi. Bu durum, bir şeylerin yanlış gittiğinin ilk ipuçlarından biriydi.
Vulcan'ı, Güneş'e yakın diğer gezegenleri de (Merkür ve Venüs) olduğu gibi gözlemlemenin en iyi yollarından birinin tam Güneş tutulmaları olduğunu bilen astronomi alemi 29 Temmuz 1878'de gerçekleşecek olan Güneş tutulmasını iple çekiyordu. Bu tutulma esnasında Vulcan tekrar görüldü ve önemli kayıtları yapıldı (Watson'un gözlemleri). Aslında Watson'un gözlediği gezegen de Merkür'ün düzensizliğine tek başına sebep olamayacak kadar küçüktü, ancak astronomlar arasında keşfedilmeyi bekleyen diğer gezegenlerin de aşikar olduğuna dair bir inanç vardı. Aynı şekilde Lewis Swift de tutulma sonrasında Vulcan'ı gözlemlediğini duyuranlar arasındaydı.
 |
| 1878 Güneş tutulması sonrası Watson'un gözlemleri üzerine bir haber (Kaynak: New York Times, 1878) |
Bu tutulma aynı zamanda yavaş yavaş çatlak seslerin ve itirazların ortaya çıkmasına ön ayak oldu. Princeton'lu C. A. Young, Watson'un gözlemleri konusundaki şüphelerini dile getirmişti. Tam olarak aynı anda aynı yeri inceleyen diğer önemli astronomların gözlemlerine atıf yapan Young, bu astronomların hiç birinin Watson'un iddia ettiği yerde Vulcan'ı göremediğini belirtiyor ve Watson'un gözlemlerine kuşkuyla yaklaşıyordu. Watson ise Young'ı eleştirmişti: ona göre bu astronomların yaptığı "negatif kanıt sunarak keşfi engellemekti". Watson'a göre 'negatif kanıtlar' tamamen etkisizdi. Watson, tersine, Swift'in gözlemlerine atıf yaparak onun gözlemleriyle kendininkileri destekliyordu. Kendini Young ve diğerlerine karşı savunurken şöyle diyordu: "Onların gösterdiği yerlerde bilinen yıldızlar yer almıyor, dolayısıyla gözlemlediğim cismin kimliğine dair yanılıyor olamam". Ancak, sonunda Swift ve Watson'un aslında farklı cisimleri gördükleri ortaya çıkacaktı.
Vulcan takip eden 1880, 1882 ve 1883 Güneş tutulmalarında da aranmaya devam edildi. Yine astronomlar tarafından bir kaç kez görüldüğü duyuruldu. Hatta bazıları Vulcan benzeri birden fazla iç gezegen gördüğünü de açıkladı. Ancak, tüm bunlar boşunaydı. Merkür'ün günberi pozisyonunun açıklanamayan değişimi hala çözümsüzdü. Teori ve hesaplar birbirini halen tutmuyordu. En çok inanıldığı günlerde bile Vulcan aslında bu problemin çözümüne çok ufak bir katkıdan fazlasını (küçük kütlesi nedeniyle) yapamıyordu. Newton'un teorisine göre Vulcan'ın en azından Merkür ile eş kütlede olması gerekirdi. 1880'lerden sonra astronomlar yavaş yavaş Vulcan'a dair inançlarını yitirmeye başladılar ve zamanla tamamen kaybettiler.
Albert Einstein ve Genel Görelilik Teorisi
 |
| Albert Einstein (Kaynak: Wikimedia Commons) |
1905 yılında (annus mirabilis) uzay-zamanın yapısıyla ilgili Özel Görelilik Teorisini yayımlayan Einstein, 1915'e geldiğimizde ise uzun bir süredir bir çeşit kütle çekim teorisi olan Genel Görelilik Teorisi üzerinde çalışıyordu ve aynı yıl bu konudaki meşhur makalesini yayımlayarak Vulcan'ı, defalarca kez gözlemlenen, ancak son zamanlarda varlığına dair umutların azaldığı hayali gezegeni, çalışma masasından yok etmeyi başarmıştı. Bunu, o güne kadar ki tüm zorlu sınamalardan başarıyla çıkan Newton mekaniğini (ve kütle çekim teorisini) çürüterek yapmıştı. Evet, Vulcan veya Vulcan'a benzer gezegenler yoktu ve teori ile hesaplamaların uyuşmamasının bu seferki sebebi hatalı hesaplamalar değil, bu hesapların dayandığı teorinin yanlış olmasıydı. Artık Newton'un teorisinin yerini Einstein'ınki almalıydı. Peki Einstein'ın Genel Görelelik Teorisi neydi, ne diyordu?
Öncelikle, Einstein direkt olarak ve yalnızca Merkür'ü incelemiyordu. O, Merkür'ün yörüngesine dair problemin farkındaydı, ancak bu problemi çözmekten daha fazlası peşindeydi. O genel bir teorinin ardından koşuyor ve kendi teorisinin doğruluğunu Merkür problemi üzerinde test etmek istiyordu. Onun yeni kütle çekim teorisini içeren Genel Görelilik Teorisine göre uzaydaki objeler kütleleriyle orantılı olarak uzay-zamanda eğilip bükülmelere neden oluyordu ve uzayın geometrisinde oluşan bu bozulma netice olarak kütle çekimine yol açıyordu (Newton ise varlığının farkında olsa ve formülasyonunu yapmış olsa da hiç bir zaman kütle çekimin sebebini açıklayamadı). Yani, kütle çekimi, dev kütlelerin direkt olarak uyguladığı görünmez ve gizemli bir kuvvet değil, uzayın geometrisi ile ilgili bir durumdu. Einstein'a göre bu bükülmeler ya da bozulmalar Dünya gibi görece küçük nesneler için daha küçük olurken Güneş gibi devasa cisimler için ise çevresindeki diğer cisimlerin yörüngelerini etkileyecek kadar büyük olabiliyordu (alttaki resim). Einstein daha sonra, uzay-zamanın maddeye nasıl hareket etmesi gerektiğini ve maddenin de uzay-zamana nasıl bükülmesi gerektiğini söylediği bu düşüncesinin 'yaşamının en mutlu düşüncesi' olduğunu söyleyecekti.
 |
| Uzay-zaman, büyük küreyi Güneş, küçüğü Merkür gibi düşünün (Kaynak: The Hunt for Vulcan) |
Düşünce güzel ve mutlu olsa da kanıtlanmaya (daha doğrusu sınamalardan başarıyla çıkmaya) muhtaçtı. Merkür'ün yörüngesine dair meşhur problem bu yeni teoriyi test etmek için biçilmiş kaftandı. Einstein, Öklidyen olmayan bu geometride (bükülmüş uzay) doğru hesaplamaları yapabilmek için dönemin matematikçilerinden (Schwarzschild) destek aldıktan sonra kendi teorisine göre Güneş etrafındaki uzay-zamanda tam olarak ne gibi bir bükülme olduğunu hesaplayarak bunun Merkür'ün yörüngesi üzerinde ne gibi bir etkisi olabileceğini incelemeye başladı. Hesaplarına göre bu bükülmenin Newton mekaniğiyle yapılan hesaba göre Merkür üzerinde hızlandırıcı bir etkisi olacağı belliydi.
Einstein, gerekli tüm çalışmayı yaptıktan sonra, kendi ifadesiyle heyecan ve mutluluktan kalbinin çarpıntılarını duyduğu için çalışamadığı üç gün geçirmesine neden olacak keşfini yaptı: uzay-zamanın Güneş'in kütlesi nedeniyle bükülmesi durumunda Merkür'ün yörüngesinde gerçekleşecek olan değişim (Newton mekaniğine kıyasla) tam olarak yüz yılda 43 ark saniye kadardı. Bu sayı daha önce belirttiğim gözlem sonuçlarıyla birebir uyuyordu. İşte olmuştu. Teori ve gözlem uyuşmamış ve bu sefer var olan teori başaramamış ve yerine yeni bir teori gelmişti. Einstein'ın teorisi diğer tüm gezegenler için de tutuyordu. Güneş'in dev kütlesinden uzaklaştıkça uzay-zaman bükülmesi de azaldığı için Newton'un teorisi ile aynı sonucu verse de, Newton mekaniği Güneş'e yaklaştıkça geçersiz olmaya başlıyordu.
 |
| 1919 Güneş tutulması ve Eddington deneyi (Kaynak: New York Times, 1919) |
Einstein'ın, Merkür'ün yörüngesinin günberi problemini çözmesi Genel Görelilik Teorisi'nin ilk ve en önemli zaferlerinden biriydi. Daha sonra Venüs'ün yörüngesindeki düzensizlikleri de, bir çok farklı problemi de (1975'te Güneş sistemi dışındaki bir çift yıldız sistemine uygulandığında da yine geçerli olduğu görülmüştü) aynı şekilde açıklamak mümkün olmuştu. Teorinin en büyük kanıtlarından biri ise hemen dört yıl sonrasında, 1919 senesindeki Güneş tutulmasında Eddington tarafından elde edilmişti. Eddington tutulma sırasında Dünya'dan bakıldığında izdüşümsel konumu Güneş'e yakın olan bazı yıldızları gözlemlemiş ve bunlardan gelen fotonların Güneş'in yakınından geçip bizim gözümüze ulaşırken nasıl da Güneş etrafındaki uzay-zaman bükülmesinden etkilenerek aslında olmaları gereken yerde değil de daha farklı bir pozisyonda göründüklerini gözlemlemeyi başarabilmişti.
 |
| Eddington deneyi gazetelerde, 1919 (Inside Einsteins Mind The Enigma of Space and Time, BBC, 2015 ) |
Cevapsız Kalan Sorular
Gazetelere konu olan bu deney sonrasında Einstein da teorisi gibi dünya çapında bir üne kavuşmuştu. Artık sorularımızı yanıtlayan yeni bir teorimiz vardı ve Vulcan veya Vulcanlara ihtiyacımız kalmamıştı. Ancak yine de, geride bazı ilginç sorular cevapsız kalmıştı. En önemlisi, Lescarbault 1859'da Vulcan'ı görmediyse ne görmüştü ve uzunca bir süre izleyip kaydını tutmuştu? Lescarbault bir amatördü ve muhtemelen basitçe bir hata yapmıştı. Peki ya Watson ve Swift? Bunlar tanınmış, becerikli ve ömrünü gökyüzüne ve gök cisimlerine adamış astronomlardı ve gözlem yapmayı iyi biliyorlardı. Onlar muhtemelen gerçekten bir şey görmüşlerdi. Bunun ne olduğunu ise bilmenin bir yolu yok. Belki bilinen cisimlerden birini gördüler, belki bir asteroid, belki de bir kuyrukluyıldız. Öte yandan Vulcan'ı gördüğünü açıklayan bir çok başka astronom da vardı. Bu kadar insanın aynı hatayı yapması nasıl mümkün olmuştu? Var olmayan bir gezegen nasıl olmuş da zamanının Güneş sistemi haritalarına girmeyi başarmıştı, herkes varlığından bu kadar emin olabilmişti? Belki de Newton kanunlarına olan sonsuz inançları yüzünden Vulcan'a dair beklentileri onları yanıltmıştı ve görmek istedikleri şeyi gördüklerini düşündürtmüştü.
Sahi, en başta da dediğimiz gibi, bir şey hiç var olmamışsa kaybolabilir miydi, yoksa önce bulunması mı gerekirdi? Peki, daha önemlisi, olmayan bir şey nerede bulunurdu? Unutmayın evin anahtarından değil, Güneş sistemimizdeki koca bir gezegenden bahsediyoruz...Belki Vulcan'ın bir hayal olduğu ortaya çıkacaktı, ama O bizi nihayetinde doğrulara ulaştıran bir hayaldi. Sonunda herkese gösterecekti ki, koca bir gezegen bile insanlığın kümülatif beklentilerinden büyük olamazdı ve yine de hiç bir yanlış inancın gerçeğin karşısında sonsuza dek sağlam durması mümkün değildi.
Başlıca Kaynaklar:
1. The Ghost in Newton's Clockwork Universe - In Search of Planet Vulcan, Richard Baum & William Sheehan, 1997, Springer.
2. The Hunt for Vulcan: How Albert Einstein Destroyed a Planet and Deciphered the Universe, Thomas Levenson, 2015,
3. Feynman'ın Kayıp Dersi, Gezegenlerin Güneş Çevresindeki Hareketi, Goodstein ve Goodstein, 2003
4. Inside Einsteins Mind The Enigma of Space and Time, BBC
5. https://aether.lbl.gov/www/classes/p10/gr/PrecessionperihelionMercury.htm
6. https://www.nationalgeographic.com/news/2015/11/151104-newton-einstein-gravity-vulcan-planets-mercury-astronomy-theory-of-relativity-ngbooktalk/


Yorumlar
Yorum Gönder